今回も、前回の内容の続きである。
ちょっと前に、5年考えて解けなかった問題が反響を呼んでいた。なかなか面白い問題で、みんなが熱中するのもわかる。私もこういう問題は大好きだ。下の図の角CDEを求めよという問題である。なお辺AB=ACである。
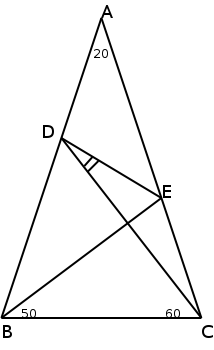
しかし、一つお願いだ。本当の中学生にこの問題を解かせないでほしい。この問題はあくまでパズルであり、本当の数学の問題ではない。こういう問題しか出さないから、子供は数学をパズルだと勘違いする。そしてこういう問題は面白いから、この面白さを数学の面白さだと勘違いする。それが良くないのだ。
「問題とは何か」という認識がまだできていない子供の頃からこういう問題ばかり目にすると、こういうものが「問題」であると勘違いする。世に言う「ひっかけ問題」「ひらめき問題」というやつのことだ。そういう問題ばかりを与えると、問題はひっかけがあったりひらめきが必要だったりするものという認識になってしまう。我々が実社会で直面する本当の問題にはひっかけもひらめきもない。普通に考えれば普通に解けるのだ。
問題は基礎を応用して理詰めで解くものである。こうしたパズルはそういうことを教えてくれず、逆に理詰めではなくひらめきを使うと簡単になると教える。だから、問題の解き方もわかってないような人にさせるのは良くないのだ。
上の問題を出されると、多くの人はあちこちの角度を図にメモし、次には適当に補助線を引き始めるだろう。この解き方こそが「パズルの解き方」であって、本当の「数学の問題の解き方」ではない。もしこの図形が機械の設計の時などに偶然出てきたとしたら、あなたは本当にあちこちの角度をメモしたり補助線を引いたりするだろうか?いくら苦労しても、そんな方法では答えは出ないかもしれないのだ。
この問題を補助線を引いて求めようとするのはあくまでこの問題に「中学生の範囲で解ける」という保証があるからである。そして実際の問題にはそんな保証はない。世の中で直面する一般の図形の問題では、補助線を引くやり方は通用しない。まあ最初のうちは少しは補助線を引いてみるかもしれないが、少しするとあきらめて正攻法で解こうとするだろう。
こういう問題の回答はたいてい「ここに補助線を引くとうまく行く」とは書いてあるが、なぜそんな所に補助線を引いたのかがきちんと説明されていない。ここに補助線を引いてみたらたまたまうまく行くからという理由だ。こんな後付けの理由は理詰めではない。こんな問題に慣れてしまっていると、解けるとわかっている問題しか解けなくなってしまう。問題解決で最初にすることは、その問題が本当に解けるかどうかを見極めることだ。解ける問題しか与えられていないとこの癖がつかなくなってしまう。
生徒には理詰めで解くことを教えよ。次のように解かせよ。
- まず座標系を設定する。例えばB点を原点にする。
- 二等辺三角形で頂角がわかっているから、三角関数を使えばB点とC点の座標がわかる。なおこれは角度だけの問題だから、どこかの辺を適当に1とおけばよい。
- 点Bの位置と角CBEがわかっているから、辺BEの直線の式が求まる。
- 同様に、辺ACの直線の式が求まる。
- すると、二直線の交点Eの座標が求まる。
- 同様に、辺DCの式とABの式から点Dの座標が求まる。
- これですべての点の座標が確定したから、この図面に関するすべての角度と長さは(逆三角関数も使えば)わかるはずである。
詳しい解き方は解法に載せる。
この解法には恣意的な部分が一つもない。三角関数、逆三角関数と直線の式がわかっていれば理詰めだけで解ける問題である。そしてどんな図形の問題でも同じようにやれば解けるし、もしこのやり方で解けないとしたらそれは前提が足りないことがわかる。なぜ解けなくてどこがわかれば解けるのかがわかる。
もちろん、この手法だと非常に計算に時間がかかる。だからもしテストに出されたら時間内に解けないかもしれない。しかしそんなことはどうだっていい。実社会に出たら、こんな問題は自分で全部解かなくても式だけ立ててあとは電卓やMathematicaに解かせればいいのだから。極端なことを言えば、方程式さえ立てればもう解けたも同然だから、わざわざ解く必要はない。重要なことは、解けるとわかっている問題を時間内に解くことではなく、解けるかどうかもわからない問題に対して自分なりに筋道をたてて考え、解き方を導き出すことである。
以前、大学の学生のプログラム演習をお手伝いしたことがあった。モーターを制御するプログラムを作るという演習だったが、そこではテキストも何もなく、学生にはパソコンとモータ制御機器を与えて「モーターを制御するプログラムを作れ」としか言わなかった。そして、「何か質問があればいくらでも答える」と言った。皆最初は戸惑ったようだが、まずは何もしないプログラムから少しずつ増やしていって、ついにはちゃんと制御するプログラムが書けた。
学生に感想を聞いてみると「非常に面白かった。初めて自分の力でプログラムを作ったような気がした」と言っていた。この演習がもしなかったとしたら、自分の力でプログラムを作ることさえ経験しないまま「プログラミングは学校で習いました」といって就職してしまっただろう。恐しいことだ。
プログラミング演習は授業でいくらでもやったはずだ。なのになぜそれが「自分の力で」ではなかったのかというと、問題が穴埋め式だったり、必要な関数や必要事項がすべてテキストに掲載されていたりしたからだ。つまり、「これだけの情報があればこの問題はできるはずだよ。さあ、やってみよう」というテキストがあったからだ。自分が直面している問題に対するすべての情報が与えられており、それだけで解けるはずだという前提があったからだ。
そういえば、大学の演習のほとんどはテキストがあって、その手順通りにやればだいたいうまく行くようになっていて、ところどころ「自分で考えよう」と空白になっているところがあった。問題は何を考えなければいけないかが明確になっていることだ。自分が何をしなければいけないかがこと細かく書かれていたから、「自分で」やった気にならなかったのだ。「自分で考えよう」と書いてあるところを自分で考えたって、これは自分でやったことではなく、ただ言われたまま考えただけだ。本当に自分でやるには、何を考えなければいけないかを考えなければいけない。
もし一番上に出した数学の問題がわからなかったとして、何を考えなければいけないのかがわかるだろうか。言い換えれば、いったい何を質問すればいいだろうか。先生は「どこかに補助線を引いてみればわかるよ」と言うしかないだろう。そうすると今度は「どこに補助線を引けばいいかをどうやって考えればいいでしょうか?」という質問になる。さて、これに答えられるだろうか?後者が「何を考えなければいけないかを考える」ということ、言い換えれば問題を自分の力で解くということだ。
自分の力では解けないような問題しか出さないから、自分の力で解こうとしなくなる。社会科の年号だって国語の熟語だって同じだ。知っていないと解けない問題しか出さないから、問題を解くためには知るしかないことになってしまう。知っていれば解けるし知っていなければ解けない。問題を解くには覚えるしかない。だから自分で考えることをしなくなってしまう。
「わかっていないなら質問しろ。黙っていてはわからん」と怒る先生がたまにいるが、生徒の気持ちがわかっていない。何がわかっていないのかわかっていないし、生徒は言われないことをする理由がないのだ。先生が「質問しろ」と言うと質問するが、それでは本当に質問したことにはならない。本当の問題は質問しないことではなく、「○○しろ」と言われないことをしないことである。
なぜこんなことになるかというと、自発的に勉強していないからである。いや、自発的に勉強させてもらえないからである。ある単元である内容を覚えさせられ、覚えたかどうかをテストで試される。ここに自発的要素の入る隙などない。そして「なぜ年号なんかを覚えなければならないんだ」「なぜこんな公式を覚えなければならないだ」といった反抗心が植えつけられる。
二次方程式の解の公式をなぜ覚えなければいけないのか。それはテストに出るからだ。なぜテストに出ると覚えなければいけないのかというと、大学に受からないからである。そしてなぜ大学に受からないといけないのかというと、いい企業に就職できないからである。確かに間違ってはいないのだが、なんか変だ。
なぜ二次方程式の解の公式を覚えなければならないのか。それは二次方程式を解く簡単な方法だからだ。なぜ二次方程式を解かなければいけないのかというと、現実の数学や物理学の問題には二次方程式で表される問題が少なくないからである。いや、数学や物理学だけじゃない。経済学にも統計学にも出てくる。だから皆覚えておくべきだ。本来こういう理由付けでなくてはならない。
「人はなぜ考えるのか」のような哲学をやれと言っているわけではない。実際に世の中で出てくる具体的な疑問や問題から出発すべきだと言っているのだ。学校で二次方程式をやる前に、二次方程式がどこで役に立つのかを教えなければいけない。ただ「二次方程式はテストに出るから覚えろ」と言うだけでは、生徒が自主的に学習するわけないだろう。
たいていの学校の授業は、まず必要な知識を全部話し、練習問題をやって、最後に応用問題として現実に即した文章題が出題されるという順番だった。これは順番が逆である。最初に(今の知識では解けるはずもない)現実に即した難しい文章問題をバーンと出して、それを自分なりに解いてみようとさせるべきだ。そして何がわからないのか、何を知ればいいのかを認識してから初めて必要な知識を教えるべきだ。
そんなことをするときっと最初は「教えてもらってないのだから、そんな問題解けるはずがないだろ」とブーイングが起きるだろうと想像する。もしそうだとすると、何か悪いものに毒されてしまっている。「教えてもらっていない問題は解けるはずがない」というのは、何かが根本的に間違っている気がする。
問題を出す時にも、問題を解くには何がわからなければいけないかがはっきりしている問題でなくてはならない。つまり、公式や定理を何も知らなくても、「あっ、こうすれば解けそう」と見当がつくようでなくてはならない。上に挙げた解答で言えば、「点Dと点Eの位置がわかれば解けそう」と考えることだ。そしてその位置を知るにはどうすればいいか。そのために三角関数と直線の交点の求め方を勉強する。こういう順番であるべきだ。
百ます計算みたいな無駄な作業に子供の時間を使わせるな。そんなことより、強いポケモンの育て方を考えさせよ。自分が考えたいと思ったことを自発的に考えさせること、問題を整理すること、そして漠然とした問題に自分なりに道筋をつけることの方がずっと大事だ。
上のポケモン云々の話は、ポケモンがどういうゲームなのかをよく知らないまま言っています。ポケモンが単に戦闘を繰り返すだけで強くなるようなクソゲーだったら、上の発言は撤回します。