解答編

以下の図の、角CDEを求めよ。ただし辺AB=ACである。

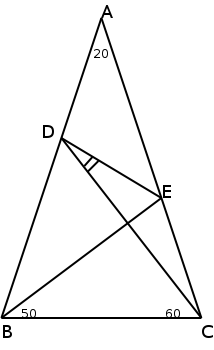
これを解くには、まず座標系を設定して、点Dと点Eの位置を計算する。それが わかれば、あとは角度を計ればいいわけだ。点Bを原点として、辺BCの距離を1 とする。すると、点A,B,Cの座標は次のようになる。(以下、角度の単位は度と するが、°は省略する)
点A: x_a=1/2, y_a=tan80/2
点B: x_b=0, y_b=0
点C: x_c=1, y_c=0

次に、点Dの座標を求める。角DBCが80°だということを使うと、辺ABの直線の 式は
y=tan80 x
辺CDの式は
y=-tan60 (x-1)
連立方程式を解いて、
x=tan60/(tan60+tan80)
tan xをsin xとcos xに分解して、加法定理を使うと
x=sin60 cos80 / (sin60 cos80+sin80 cos60)=sin60 cos80 / sin140 = sin60 cos80 / sin40
つまり、点Dは 点D: x_d=sin60 cos80 / sin40
y_d=sin80/cos80 x_d=sin 60 sin80 / sin40
点Eも同様に計算して
点E: x_e=sin80 cos50 / sin50
y_d=sin50/cos50 x_d=sin 80

これですべての点の座標がわかったので、辺DEの傾きと辺CDの傾きを知れば角 度がわかる。辺CDの傾きは60°である。辺DEの傾きkを求めるには、X軸とY軸 のそれぞれの距離を計算して割ればよい。
dx=x_e-x_d, dy=y_e-y_dとする。
dx=sin80 cos50 / sin50 - sin60 cos80 / sin40
=(sin50 + sin30)/2sin50 - (sin40 - sin20)/2sin 40
=1/2 + sin30/2sin50 - 1/2 + sin20/2sin40
=(sin30 sin40 + sin20 sin50)/2sin40 sin50
dy=sin80 - sin60 sin80 / sin40
=sin80 (sin40 - sin60)/sin40
dy/dx = 2 sin50 sin80 (sin40 - sin60) / ( sin30 sin40 + sin20 sin50)
角CDEは 辺CDの傾き角-辺DEの傾き角 = 60 - arctan(dy/dx)度である。三角関 数と逆三角関数を電卓で使えるなら、この時点で、電卓をたたけば角度はわか る。

試しに電卓でdy/dxを計算してみると、角度は30°であることがわかる。この 時点で初めて、「この式はもしかしたらもっと単純になるのかもしれない」と 思いつくはずだ。そこで、dy/dxの式を簡単にすることを考える。
dy/dx = 2 sin50 sin80 (sin40 - sin60) / ( sin30 sin40 + sin20 sin50)
= -2sin80 sin20 / (cos10 + cos30 - 2cos 70) (積和、和積の公式を使って 整理)
= -2cos10 sin20 / (2cos20 cos10 - 2sin 20)
= -cos10 sin20 / (cos20 cos10 - 2cos 10 sin10)
= -sin20 / (cos20 - 2sin10)
= -sin20 / (cos20 - cos80 - sin10)
= -sin20 / (2sin 50 sin 30 - sin 10)
= -sin20 / (sin50 - sin10) (sin30=1/2より)
= -sin20 / (2cos 30 sin 20)
= -1/2cos 30
= -sin30 / cos 30
= -tan 30
というわけで、角CDE は 60-30 = 30度である。